Zbiorem wszystkich rozwiązań nierówności 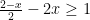jest przedział
A. ⟨0, +∞)
B. (−∞, 0⟩
C. (−∞, 5⟩
D. (−∞, ⅓⟩
Źródło CKE - Arkusz egzaminacyjny 2020/2021 - Matura maj (05.05.2021) poziom podstawowy
Analiza:
Rozwiążmy nierówność. Pozbądźmy się ułamka mnożąc obustronnie przez 2.
Stąd otrzymujemy (−∞, 0⟩.
Odpowiedź:
A. ⟨0, +∞)
B. (−∞, 0⟩
C. (−∞, 5⟩
D. (−∞, ⅓⟩
Matura maj 2021 playlista
Zadanie 6 - wersja video
Matura - poziom podstawowy
Egzaminy maturalne - archiwum
2017
Zadania z matury podstawowej z matematyki 2016 są obecnie wprowadzane na stronę. W niedługim czasie udostępnione zostaną odpowiedzi i analizy zadań.
Zadanie z odpowiedzią bez analizy
Zadanie z analizą i odpowiedzią
2016
Zadania z matury podstawowej z matematyki 2016 są obecnie wprowadzane na stronę. W niedługim czasie udostępnione zostaną odpowiedzi i analizy zadań.
Zadanie z odpowiedzią bez analizy
Zadanie z analizą i odpowiedzią
2015
Zadania z matury podstawowej z matematyki 2015 są obecnie wprowadzane na stronę. W niedługim czasie udostępnione zostaną odpowiedzi i analizy zadań.
Zadanie chwilowo niedostępne
Zadanie z odpowiedzią bez analizy
Zadanie z analizą i odpowiedzią
2014
Egzamin maturalny w starej formule. Zadania z matury podstawowej z matematyki 2014 są obecnie wprowadzane na stronę. W niedługim czasie udostępnione zostaną odpowiedzi i analizy zadań.
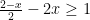jest przedział 
