Zadanie 17 (0-1) - matura poziom podstawowy sierpień 2023, zadanie 17
2023
Dany jest ciąg geometryczny (an ), określony dla każdej liczby naturalnej n≥1. Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe. Wyraz a2023 jest liczbą ujemną. P F Różnica a3 −a2 jest równa 96. P F
Źródło CKE - Arkusz egzaminacyjny 2022/2023 - Matura czerwiec (22.08.2023) poziom podstawowy
Analiza:
Możemy skorzystać z wzoru ogólnego na n-ty wyraz ciągu:
Podnosimy liczbę ujemną do potęgi o wykładniku parzystym: 2023 jest dodatnie.
Policzmy:
Sąd różnica:
a3 -a2 =32-(-64)=32+64=96
Odpowiedź:
Wyraz a2023 jest liczbą ujemną. P F Różnica a3 −a2 jest równa 96. P F
Poziom szkoły średniej (poziom podstawowy)
Funkcja liniowa i równanie prostej
Proste, punkty, odcinki (geometria na płaszczyźnie kartezjańskiej)
Kąt wpisany i kąt środkowy w okręgu
Mediana i średnia arytmetyczna
Rachunek prawdopodobieństwa
Poziom szkoły średniej (poziom rozszerzony)
Maj 2024
Czerwiec 2024
Sierpień 2024
Grudzień 2024
Informator 2025
Maj 2023
Czerwiec 2023
Sierpień 2023
Wrzesień 2022
Grudzień 2022
Maj 2022
Czerwiec 2022
Sierpień 2022
Marzec 2021
Maj 2021
Czerwiec 2021
Sierpień 2021
Maj 2020
Czerwiec 2020
Sierpień 2020
Maj 2019
Czerwiec 2019
Sierpień 2019
Czerwiec 2018
Sierpień 2018
Maj 2017
Czerwiec 2017
Sierpień 2017
Maj 2016
Czerwiec 2016
Sierpień 2016
Maj 2015
Czerwiec 2015
Sierpień 2015
Maj 2014
Czerwiec 2014
Sierpień 2014
Maj 2013
Czerwiec 2013
Sierpień 2013
Maj 2012
Czerwiec 2012
Sierpień 2012
Maj 2011
Czerwiec 2011
Sierpień 2011
Maj 2010
Czerwiec 2010
Sierpień 2010
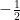
jest dodatnie. Przemnożenie tej dodatniej liczby przez 128, które jest dodatnie nie zmienia już sytuacji. Zatem a2023 jest dodatnie.


