Zadanie 3 (0-1) |
Wskaż liczbę spełniającą nierówność (4-x)(x+3)(x+4)>0
A. 5
B. 16
C. -4
D. -2
Źródło CKE - Arkusz egzaminacyjny 2017/2018 - Matura czerwiec poziom podstawowy
Analiza:
Formalny
Mamy do czynienia z wielomianem, którego pierwiastki są następujące: 4, -3, -4. Aby rozwiązać nierówność narysujemy sobie wykres wielomianu. Do tego będziemy potrzebowali jeszcze znak przy wyrazie wielomianu z najwyższą potęgą:
(4-x)(x+3)(x+4)>0
(4-x)(4+x)(x+3)>0
(16-x2)(x+3)>0
16x-x3-3x2+48>0
-x3-3x2+16x+48>0
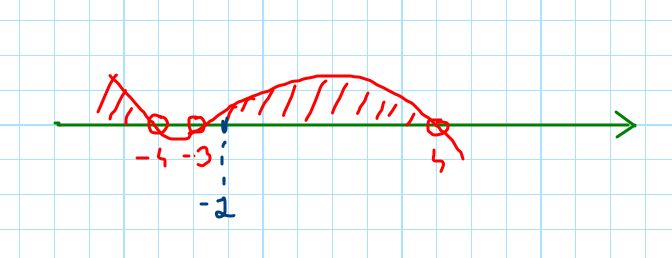
Zaznaczmy miejsca zerowe na osi:

Wyraz z najwyższą potęgą jest ujemny, dlatego zaczynamy rysować wykres z prawej strony od dołu:

Zaznaczmy przedziały dla których spełniona jest nierówność.

Tylko -2 należy do rozwiązania nierówności.