|
Zadanie 3 (0-1) - matura poziom podstawowy sierpień 2023, zadanie 3
|
2023
|
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 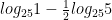 jest równa
jest równa
Źródło CKE - Arkusz egzaminacyjny 2022/2023 - Matura czerwiec (22.08.2023) poziom podstawowy
Analiza:
Skorzystajmy z własności:
nlogab=logabn


Oba logarytmy mają tą samą podstawę, dlatego też możemy skorzystać z kolejnej własności:



Ponownie skorzystajmy z:
logabn=nlogab



Odpowiedź:
Poziom szkoły średniej (poziom podstawowy)
Funkcja liniowa i równanie prostej
Proste, punkty, odcinki (geometria na płaszczyźnie kartezjańskiej)
Kąt wpisany i kąt środkowy w okręgu
Mediana i średnia arytmetyczna
Rachunek prawdopodobieństwa
Poziom szkoły średniej (poziom rozszerzony)
Maj 2024
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2024
Zadanie z odpowiedzią - bez analizy
Zadanie bez odpowiedzi i bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2024
Zadanie z odpowiedzią - bez analizy
Zadanie bez odpowiedzi i bez analizy
Zadanie z analizą i odpowiedzią
Grudzień 2024
Zadanie z odpowiedzią - bez analizy
Zadanie bez odpowiedzi i bez analizy
Zadanie z analizą i odpowiedzią
Informator 2025
Zadanie z odpowiedzią - bez analizy
Zadanie bez odpowiedzi i bez analizy
Zadanie z analizą i odpowiedzią
Maj 2023
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2023
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2023
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Wrzesień 2022
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Grudzień 2022
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Maj 2022
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2022
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2022
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Marzec 2021
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Maj 2021
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2021
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2021
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Maj 2020
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2020
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2020
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Maj 2019
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2019
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2019
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2018
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2018
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Maj 2017
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2017
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2017
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2016
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2016
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Sierpień 2016
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie z analizą i odpowiedzią
Maj 2015
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2015
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2015
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2014
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2014
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2014
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2013
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2013
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2013
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2012
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2012
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2012
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2011
Zadanie dowodowe bez analizy
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2011
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2011
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Maj 2010
Zadanie z odpowiedzią - bez analizy
Zadanie z analizą i odpowiedzią
Czerwiec 2010
Zadanie z odpowiedzią - bez analizy
Zadanie dowodowe bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
Sierpień 2010
Zadanie z odpowiedzią - bez analizy
Zadanie bez analizy i odpowiedzi
Zadanie z analizą i odpowiedzią
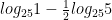 jest równa
jest równa

