Trochę przewrotny tytuł, ponieważ kwadrat także jest rombem, w którym wszystkie kąty są proste.
Wśród istotnych parametrów opisujących te dwa czworokąty są: pole i obwód. Przyjrzyjmy się najpierw obwodowi. Zarówno w kwadracie jak i w rombie i w innych wielokątach) obwód to suma długości wszystkich boków. Ponieważ romb i kwadrat mają cztery boki o tej samej długości, to ich obwód jest równy (przy założeniu, że obie figury mają boki o długości a):


A co z polem?
Równanie opisujące pole rombu:

gdzie a to długość boku, h to długość wysokości prostopadłej do boku a. W rombie wszystkie wysokości mają tą samą długość (zobacz graficzny eksperyment - link do karty).
Na karcie:
Aby zmienić długość wysokości skorzystaj z pomarańczowego wierzchołka.
Zmieniając jego położenie, zmieniasz wartość wysokości.
Po obejrzeniu animacji powinieneś zauważyć, że wszystkie wysokości rombu w każdej sytuacji są sobie równe. Gdy nasz romb staje się kwadratem, to wysokość jest równa długości boku.
Stąd pole kwadratu jest równe:
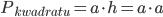
Już powinieneś zauważyć pewną zależność. Obwód dla rombu i kwadratu o bokach a jest ten sam, ale pole już nie. Spójrz na symulację poniżej (link do karty masz TU).
Na karcie:
Aby zmienić długość wysokości skorzystaj z pomarańczowego wierzchołka.
Zmieniając jego położenie, zmieniasz wartość wysokości.
Maksymalną wartość pola osiąga romb, który jest kwadratem :-). Reszta rombów o tym samym boku a ma pola zawarte między zerem a polem kwadratu o tej samej długości boku.


