|
Zadanie 17 (0-1) - matura poziom podstawowy sierpień 2023, zadanie 17 |
2023 |
Dany jest ciąg geometryczny (an), określony dla każdej liczby naturalnej n≥1. Pierwszy wyraz tego ciągu jest równy 128, natomiast iloraz ciągu jest równy 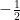
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Wyraz a2023 jest liczbą ujemną. | P | F |
| Różnica a3−a2 jest równa 96. | P | F |
Źródło CKE - Arkusz egzaminacyjny 2022/2023 - Matura czerwiec (22.08.2023) poziom podstawowy






